INEQUALITIES ↠ An inequality is like an equation that uses symbols for "less than"(<) and "greater than"(>) where an equation uses a symbol for "is equal to" (=).

HOW TO SOLVE?
Solving inequalities is very like solving equations, BUT we must also pay attention to the direction of the inequality.
Direction: Which way the arrow "points"
Some things can change the direction .
< becomes >
> becomes <
≤ becomes ≥
≥ becomes ≤
These things do not affect the direction of the inequality:
- Add (or subtract) a number from both sides
- Multiply (or divide) both sides by a positive number
- Simplify a side
Example : 3x < 7+3
We can simplify 7+3 without affecting the inequality:
3x < 10
These things change the direction of the inequality ("<" becomes ">" for example):
- Multiply (or divide) both sides by a negative number
- Swapping left and right hand sides
Example: 2y+7 < 12
When we swap the left and right hand sides, we must also change the direction of the inequality:
12 > 2y+7
↠ ADDING OR SUBTRACTING A VALUE ↞
We can often solve inequalities by adding or subtracting a number from both sides (just as in introduction to algebra), like this:
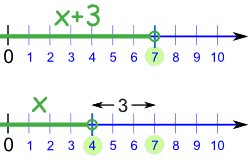
Solve: x + 3 < 7
If we subtract 3 from both sides, we get:
x + 3 - 3 < 7 - 3
x < 4
And that is our solution: x < 4
In other words, x can be any value less than 4.
What did we do?
We went from this:
To this:
|  |
x+3 < 7
x < 4
|
↠Multiplying or Dividing by a Value↞
Another thing we do is multiply or divide both sides by a value (just as in Algebra - Multiplying).
But we need to be a bit more careful!
⇛Positive Values
Everything is fine if we want to multiply or divide by a positive number:
solve: 3y < 15
If we divide both sides by 3 we get:
3y/3 < 15/3
y < 5
And that is our solution: y < 5
⇛Negative Values
when we hen we multiply or divide by a negative number
we must reverse the inequality.

No comments:
Post a Comment